引言

面对金融危机，人们能做的事情很少，但每次危机都是一个让我们重新思考自己风险管理策略的机会。在过去的几十年里，危机的强度（不是频率）有增强的趋势。因此，能够应对极端市场条件的投资策略已变得越来越重要。正如纳西姆-塔勒布在其畅销书《黑天鹅》中所解释的那样，面对将要发生的危机我们应“考虑如何应对，而不是试图去预测。”

塔勒布在他随后出版的开创性著作《反脆弱》中提出了这种应对的办法，解释了具有“反脆弱性”的系统如何不仅能够承受不确定性、冲击和破坏，还能从这些逆境中获益。他写道：“风能熄灭蜡烛，也能激发火焰”“同样，随机性、不确定性、混乱也是如此：你要利用它们，而不是躲避它们。你要成为迎接风的火。” 按照塔勒布的定义，通常情况下应对压力所产生反应是凸性的（Convex）系统是反脆弱的，而那些反应为凹性的（Concave）系统是脆弱的。本文通过对投资策略，市场泡沫以及金融危机的总结分析，进一步探讨了如何预判危机并建立具有“反脆弱性”的投资组合。

主流框架：布莱克-利特曼（Black-Litterman）和马科维茨（Markowitz）

当前，全球绝大多数的长期资产管理策略都是在Black-Litterman框架内进行的（Black & Litterman, 1991）。这个框架将马科维茨（Markowitz）的均值-方差优化目标置于贝叶斯统计（Bayesian statistics）的背景下。换句话说，虽然目标仍然是最大化夏普比率 (Sharpe, 1966)，但对投资组合各成分的预期收益、波动性和相关性的估计被纳入优化算法中。

通常为了进行贝叶斯统计计算，需要一个“先验分布”，在没有其他信息时Black-Litterman会做出先验假设，即假设某些主要市场指数（例如美国的标普500）已经是最优的组合。因此，任何偏离这一假设的情况都被视为投资人施加的 “观点”。这些 “观点”可以是数据驱动的（从价格的历史时间序列中观察到的统计规律），也可以是基于任何种类的经济分析，或者是两者的混合。与马科维茨算法不同，Black-Litterman模型更稳定，而且投资者“观点”可以以相当直观的方式应用：如果你预期某个行业会上升，投资组合自然会超额配置这个行业，如果你完全没有观点，那么模型给出的最佳投资组合就会变成一个简单的被动投资组合。

这类模型也适用于分阶段性的投资过程：先在资产类别（股票、固定收益等）之间进行战略选择，然后在特定资产中对各个行业进行具体配置。正是基于其应用的便利性，Black-Litterman投资框架在业界备受追捧，据统计，目前全球超过一半的资产管理机构都利用类似的框架进行投资。

然而，正如明斯基(Minsky H. , 1992)所观察到的那样，市场作为一个复杂的系统，可能会因为一些随机的原因对自身的不稳定性做出反应。例如，如果一个行业的估值开始上升，Black-Litterman模型将根据市场平衡理论把这种价格上涨视为有效信息，并将建议跟随它，从而加强这种趋势，而这种动态趋势则可能会演变成一个纯粹的投机性泡沫。

以美国的医疗保健行业为例（图1），医保行业的上升趋势从2011年缓慢形成，在2014年6月快速加强，随后在2015年8月被逆转，而趋势逆转的原因是看似跟美国医保行业无关的事件：中国股市泡沫的破灭。在2011年，这个行业相对于其他行业的超额表现是基于其更高的经济效益，然而这种上涨吸引了由Black-Litterman模型驱动的资本流入，推高了医疗保健行业的定价。在一些随机的负面刺激下，该板块形成超跌，最终撤回了其相对于标准普尔500指数的所有超额收益。

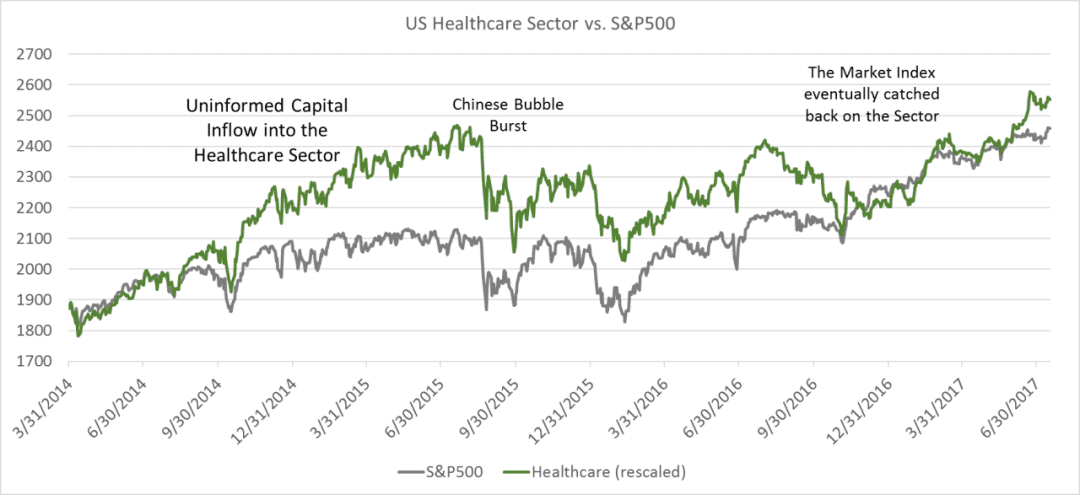
（图1 美国医保行业与标普500）

这个例子阐明了Black-Litterman方法的弱点。这种资产配置模型过于依赖于一个均衡的假设，即 “市场总是正确的”。由于该模型本质上是基于均值-方差分析，因此会受到区间变化和“黑天鹅”事件的影响。基于这类模型来优化投资组合，很难保持优异持久的投资业绩。

投机泡沫与信用危机

事实上，大多数金融危机是由于投机泡沫或信贷收缩这类内部因素而产生的，近年来只有新冠疫情、9/11事件、神户地震和福岛事故这些外部刺激对市场产生了较明显的影响。

1.投机泡沫的产生与破灭

起初，不管是出于怎样的原因，一些宏观经济领域或行业板块开始吸引资本。这个阶段对经济非常重要，因为它是价值创造和创新融资的核心引擎。然后是第二个阶段，在这个阶段，那些害怕错过的人开始大规模投资，他们比第一阶段的投资者更缺乏鉴别能力。这便是投机性泡沫的开始：资金流向利润较低的投资，其资本价值的增加来自于需求，而不是其实际盈利能力。投资者购买资产不是因为它们有吸引力，而是因为他们希望能够以更高的价格出售，当音乐停止时，我们都知道故事的结局。图2是2000年美国互联网泡沫破灭和2015年中国股市危机的历史叠加。

（图2 互联网泡沫与2015中国股市泡沫 ）

如上图所示，在两个不同的时期，两个不同的国家，却有着极其相似的泡沫模式，以至于我们不需要对数据做任何缩放。Sornette和Cauwells（Sornette & Cauwells，2015）通过价格的“超指数增长”来识别投机性泡沫，即增长率本身呈指数型增长。正如我们在这两次相似泡沫中所看到的，增长率分阶段递增，与投资者的行为相一致，最终增长率达到了不可持续和不现实的水平。识别精确的“超指数增长”阶段是难以达成的，但尽早识别泡沫的出现以安全地远离它是可能的：如果对指数的组成部分进行更准确的观察，会发现一个非对称效应：不是所有的股票都以同样的速度上升，但下跌却更加联动，从而产生了个别股票对指数的非线性反应。这种现象类似于“卖出认沽期权”--是市场紧张的典型标志。

2. 信用危机

信用泡沫是另一种市场失衡，它不应与投机性泡沫混为一谈。在投机泡沫中，出现偏差的是股票估值，而在信贷泡沫中，是公司的杠杆率造成了通常所说的 “明斯基时刻”。在信用泡沫初期，利率很低，信贷限额很宽松，公司保持在“对冲”区域的同时，对借入重大数额的资金感到放心。然而当经济周期的演变导致收益率下降时，债务负担就会加重，借款人则可能会从“对冲”区经过“投机”区最后转移到“庞氏”区。当整个企业部门或某些特定产业部门的全球杠杆率上升，就会出现信贷泡沫。图3是1998年俄罗斯危机与2008年美国次贷危机的比较。

（图3 俄罗斯金融危机 美国次贷危机）

与投机性泡沫不同的是，信贷泡沫中泡沫前后的收益数据是不对称的，这源于债务资产的价格是有边界的。值得注意的是，中国经济近年来经历了大规模的信贷泡沫以及随后的“去杠杆”阶段，然而2015年的股市危机却是一个典型的由外部资本流入产生的投机性泡沫。

如何预测危机并建立“反脆弱性”的投资组合

如前文所提到，基于均值-方差分析的优化框架（如Black-Litterman和马科维茨）忽略了市场的区间变化，这样可能积累更大的尾部风险，并让投资组合更容易收到“黑天鹅”事件的影响。一个被优化的投资组合中的资产在低波动率市场环境下可能具备很低的相关性，但一旦在高波动率情景下，组合中的资产会呈现出极高的相关性，组合的收益来源可能从阿尔法（α）完全转变为贝塔（β）。由此可见，建立具有韧性甚至是反脆弱性的组合是至关重要的，它能让投资者在金融危机或区间变化中减小损失甚至获益。正如塔勒布所提到，应对压力所产生反应是凸性（Convex）的投资体系是反脆弱的。通常来讲，凸性可以通过两种方式实现：1. 投资于那些对市场走势天然具有凸性反应的金融资产。2. 根据市场趋势动态地调整组合来规避风险。

第一种方法主要涉及期权交易。期权的报酬函数相对于其绑定资产的价格波动是具有凸性反应的。投资者可以通过在组合中加入看跌期权来实现这种凸性，然而这种保护可能相当昂贵并严重影响业绩。通过卖出看涨期权来资助保护性看跌期权是另一种具有凸性的策略，但这种策略的代价是放弃“向上的黑天鹅”，它在长期投资业绩中也会产生不小的负面影响。

第二种方法看似容易，但如果等待市场趋势形成后再作出调整，结果往往是不理想的。这种动态调整必须具备前瞻性。我们不能精准预测“黑天鹅”何时会降临，但我们可以检验市场是否更容易发生“黑天鹅”事件。通过衡量市场的不稳定性和系统性风险，有效的选择行业或资产，控制尾部事件对组合的影响，从而达到卓越的长期回报。

主导因子分析Dominant Factor Analysis (DFA)

主导因子分析（DFA）是一种具备前瞻性的风险预测方法，它使用非线性多变量模型来估计一项投资或一个投资组合的风险。其原理是通过为每个环境风险因子拟合不同的非线性模型，将投资回报与大量的潜在风险因素进行比较。为了避免过度拟合，传统的多因子模型被限制为线性模型，因此不能适应区间动态变化，而非线性模型可以在模型中纳入区间的变化。每个因子都被赋予一个分数，对应于它与某项投资的拟合程度。只有得分足够高的因子被保留（即主导因子）。对于每个主导因子，将这项投资与之进行拟合可以得到一个脉冲响应函数（IRF），然后把该因子在过去经历的危机映射到该项投资中。

（图4 DFA危机预测指标与标普500）

这种方法为这项投资生成了一个代表其风险概况的极端情景列表。在金融危机前，风险因子之间的关联性增强，主导因子的数量增加，从而加强了极端风险的概率。图4展示了通过主导因子得分总和建立的危机预测指标。更加重要的是，主导因子分析（DFA）提供了比较不同投资应对风险反应的方法，投资者可将不同标的根据其风险概况和凸性程度（源自非线性回归）排名，从而挑选出具有 “反脆弱性”的投资组合。其核心原则主要在于以下三点：

1.市场存在尾部风险聚集（Tail-Concentration）效应，这种情况一旦出现，基于历史数据估计的线性相关性系数将完全失效。

2. 风险来源很难被精准定位，因此有必要监测尽可能多的环境风险因子，这一数量可能会远远多过普通的多因子模型所用到的因子数量。

3. 风险因子与投资组合之间同样存在非线性关系，贝塔（β）系数是随时间变化的，因此即使组合中没有非线性资产，也需要用到高阶关系式，而不是简单的阿尔法（α）和贝塔（β）。

结论

金融市场基本上是由趋势、泡沫、恐惧、过度反应以及“羊群效应”所驱动，基于收益-方差构建的投资组合往往低估了这些情况对整体预期的影响，而传统的优化模型则忽略了市场区间的动态变化，反而可能加重这样的负面影响。本文提出了如何利用主导因子分析（DFA）这类前瞻性方法预测金融危机，并建立具有“反脆弱性”的投资组合来保证持久卓越的投资业绩。

文献参考

Black, F., & Litterman, R. B. (1991, September). Asset Allocation Combining Investor Views withMarket Equilibrium. The Journal of Fixed Income, 1(2), pp. 7-18.

Bollerslev, T. (1986). Generalized Autoregressive Conditional Heteroskedasticity.

Journal of Econometrics, 31(3), pp. 307-327.

Coste, C., Douady, R., & Zovko, I. (2011). The Stress VaR: A New Risk Concept for Extreme Risk and Fund Allocation. Journal of Alternative Investments, 13(3), pp. 10-23.

Douady, R. (2017, October 9). Dominant Factor Analysis by Nonlinear Polymodels. Retrieved from MCFAM Distinguished Lectures, University of Minnesota:

Douady, R., & Ye, X. (2019). Systemic Risk Indicators Based on Nonlinear PolyModel. J. Risk Financial Manag., 12(2), pp. 1-24.

Markowitz, H. M. (1991). Portfolio Selection: Efficient Diversification of Investments (2nd ed.).Minsky, H. (1992). The Financial Instability Hypothesis. Levy Economic Institute of Bard College Working Paper, 74, pp. 6-8.

Sornette, D., & Cauwells, P. (2015). Financial Bubbles: Mechanisms and Diagnostics. Review of Behavioral Economics, 2(3), pp. 279-305.

Taleb, N. N. (2000). The Black Swan. Random House.

Taleb, N. N. (2012). Antifragile: Things That Gain from Disorder. Random House.

Taleb, N. N., & Douady, R. (2013). Mathematical definition, mapping, and detection of (anti)fragility. Quantitative Finance, 13(11), pp. 1677-1689.